Try our free TSIA2 Math practice test. This online test covers all of the topics that are found on the latest version of the Texas Success Initiative Assessment. It includes 20 challenging practice questions with answers and detailed explanations. There is no time limit for this test and you may use a calculator.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Pierre randomly picks out and keeps a marble from a bag that contains 4 red marbles, 7 blue marbles, 9 yellow marbles, and 6 green marbles. Then Antoine picks a marble at random from the same bag.
If Pierre’s marble is green, what is the probability that Antoine’s marble will also be green?
$\dfrac{6}{26}$ | |
$\dfrac{5}{26}$ | |
$\dfrac{3}{13}$ | |
$\dfrac{1}{5}$ |
Question 1 Explanation:
The correct answer is (D). Since Pierre keeps his marble, the number of green marbles and the total number of marbles both decrease by 1. So there will be 5 green marbles and 25 total marbles:
$\text{Probability}$ $= \dfrac{5}{25} = \dfrac{1}{5}$
$\text{Probability}$ $= \dfrac{5}{25} = \dfrac{1}{5}$
Question 2 |
In the coordinate plane shown below, what point represents (−1, 3)?
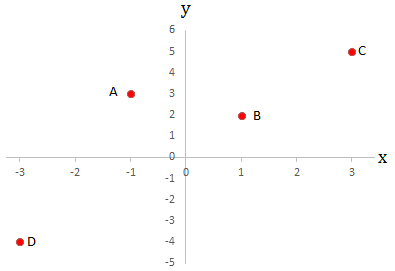
A | |
B | |
C | |
D |
Question 2 Explanation:
The correct answer is (A). Recall that the coordinate plane has a horizontal x axis and a vertical y axis that intersect at the point (0,0). The x values along the x axis increase to the right and decrease to the left, with negative values to the left of 0. The y values along the y axis increase vertically upwards and decrease vertically downwards, with negative values below 0.
The point (−1, 3) is then 1 unit to the left of (0, 0), and 3 units upwards from (−1, 0). This is represented by point A on the coordinate plane.
The point (−1, 3) is then 1 unit to the left of (0, 0), and 3 units upwards from (−1, 0). This is represented by point A on the coordinate plane.
Question 3 |
A beverage company would like to test the reliability of two processes for producing orange juice and apple cider, respectively. A review of the orange juice production process found that 10% of the bottles are under-filled. A review of the apple cider production process found that 15% of the bottles are under-filled.
If two bottles are selected at random (one from each process), what is the probability of selecting one under-filled orange juice bottle and one under-filled apple cider bottle?

0.015 | |
0.10 | |
0.15 | |
0.25 |
Question 3 Explanation:
The correct answer is (A).
Let P(A) be the probability of selecting an under filled orange juice bottle.
Let P(B) be the probability of selecting an under filled apple cider bottle.
For independent events, those that do not influence the probability of the other occurring, the probability of events A and B occurring is given by the formula:
$P(A \text{ and } B) = P(A) \ast P(B)$
The two events are independent because selecting an under filled bottle from the orange juice lot does not affect the probability of selecting an under filled bottle from the apple cider lot. Substitute the given values and evaluate their product to find the probability of selecting both:
$P(A \text{ and } B) = 0.10 \ast 0.15$
$P(A \text{ and } B) = 0.015$
Let P(A) be the probability of selecting an under filled orange juice bottle.
Let P(B) be the probability of selecting an under filled apple cider bottle.
For independent events, those that do not influence the probability of the other occurring, the probability of events A and B occurring is given by the formula:
$P(A \text{ and } B) = P(A) \ast P(B)$
The two events are independent because selecting an under filled bottle from the orange juice lot does not affect the probability of selecting an under filled bottle from the apple cider lot. Substitute the given values and evaluate their product to find the probability of selecting both:
$P(A \text{ and } B) = 0.10 \ast 0.15$
$P(A \text{ and } B) = 0.015$
Question 4 |
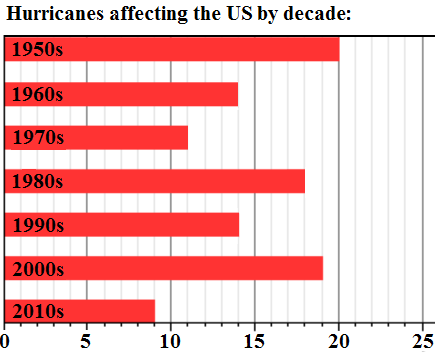
What is the mean number of hurricanes affecting the US per decade?
13 | |
14 | |
15 | |
18 |
Question 4 Explanation:
The correct answer is (C). Mean is just another word for average. To find the average, add up all the numbers, then divide by how many numbers there are:
$\text{Avg} =$ $\frac{20 + 14 + 11 + 18 + 14 + 19 + 9}{7}$
$\text{Avg} = \frac{105}{7} = 15$
$\text{Avg} =$ $\frac{20 + 14 + 11 + 18 + 14 + 19 + 9}{7}$
$\text{Avg} = \frac{105}{7} = 15$
Question 5 |
$12−\sqrt{3x}=8$
Solve for $x$.
$\sqrt{20}$ | |
$4$ | |
$\dfrac{16}{3}$ | |
$\dfrac{4}{3}$ |
Question 5 Explanation:
The correct answer is (C). Begin by isolating the radical (“get the square root part by itself”):
$12−\sqrt{3x}=8$
$12−8=\sqrt{3x}$
$4=\sqrt{3x}$
To get rid of the square root, we need to square both sides:
$(4)^2=(\sqrt{3x})^2$
$16=3x$
$x=\dfrac{16}{3}$
$12−\sqrt{3x}=8$
$12−8=\sqrt{3x}$
$4=\sqrt{3x}$
To get rid of the square root, we need to square both sides:
$(4)^2=(\sqrt{3x})^2$
$16=3x$
$x=\dfrac{16}{3}$
Question 6 |
If Tonya needed to buy 9 bottles of soda for a party in which 12 people attended, how many bottles of soda will she need to buy for a party in which 8 people are attending?
6 | |
8 | |
10 | |
12 |
Question 6 Explanation:
The correct answer is (A). We can set up a proportion to solve:
$\dfrac{9 \text{ bottles}}{12 \text{ people}} = \dfrac {x \text{ bottles}}{8 \text{ people}}$
Cross-multiply to solve a proportion:
$(9)(8) = (12)(x)$
$72 = 12x$
$6 = x$
$\dfrac{9 \text{ bottles}}{12 \text{ people}} = \dfrac {x \text{ bottles}}{8 \text{ people}}$
Cross-multiply to solve a proportion:
$(9)(8) = (12)(x)$
$72 = 12x$
$6 = x$
Question 7 |
$f(x)=(3−x)(x+3)$. What is the value of $f(−5)$?
−16 | |
4 | |
−4 | |
64 |
Question 7 Explanation:
The correct answer is (A). To find $f(−5)$, we need to plug in $−5$ everywhere we see $x$ in the original expression:
$f(−5)=(3− −5)(−5+3)$
$=(3+5)(−5+3)$
$=(8)(−2)$
$=−16$
$f(−5)=(3− −5)(−5+3)$
$=(3+5)(−5+3)$
$=(8)(−2)$
$=−16$
Question 8 |
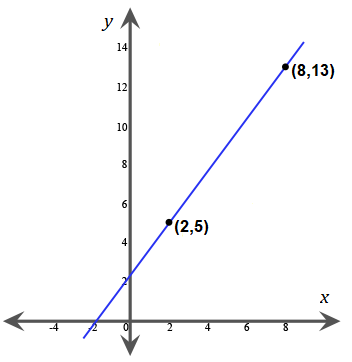
What is the equation of a line parallel to the one shown above?
$y = \dfrac{4}{3}x + 7$ | |
$y = 2x + 7$ | |
$y = 5x + 8$ | |
$y = \dfrac{3}{4}x + \dfrac{7}{3}$ |
Question 8 Explanation:
The correct answer is (A). Use the slope formula:
$\text{Slope} = \dfrac{\text{Change in } y}{\text{Change in } x}$ $= \dfrac{y_2 − y_1}{x_2 − x_1}$
The slope of the line that is pictured is:
$\dfrac{13 − 5}{8 − 2} = \dfrac{8}{6} = \dfrac{4}{3}$
Each of the answer choices is written in slope-intercept form, $y = mx + b$, where $m$ is the slope. Only one choice has a slope of $\frac{4}{3}$.
$\text{Slope} = \dfrac{\text{Change in } y}{\text{Change in } x}$ $= \dfrac{y_2 − y_1}{x_2 − x_1}$
The slope of the line that is pictured is:
$\dfrac{13 − 5}{8 − 2} = \dfrac{8}{6} = \dfrac{4}{3}$
Each of the answer choices is written in slope-intercept form, $y = mx + b$, where $m$ is the slope. Only one choice has a slope of $\frac{4}{3}$.
Question 9 |
Consider the list:
2, 2, 3, 5, 9, 11, 17, 21
If the number 23 is added to the list, which measurement will NOT change?
Mean | |
Median | |
Mode | |
Range |
Question 9 Explanation:
The correct answer is (C). The mode will not change. The mode is the number that appears the most frequently; in this case it is 2. The remaining measures will change:
The mean is the average, and in this case, it will increase because a number larger than the current average is added to the list.
The median is the number in the middle, and it will change from 7 to 9.
The range is the difference between the highest and lowest numbers and will change from 19 to 21 because a new maximum value is added to the list (21 − 2 = 19 and 23 − 2 = 21).
The mean is the average, and in this case, it will increase because a number larger than the current average is added to the list.
The median is the number in the middle, and it will change from 7 to 9.
The range is the difference between the highest and lowest numbers and will change from 19 to 21 because a new maximum value is added to the list (21 − 2 = 19 and 23 − 2 = 21).
Question 10 |
The length of a rectangle is four more than its width. If the area of the rectangle is 12, find the length of the rectangle.
−6 | |
2 | |
4.5 | |
6 |
Question 10 Explanation:
The correct answer is (D). Since the length of the rectangle is four more than the rectangle’s width:
$l = w + 4$
Substituting in $w + 4$ for $l$ and $12$ for $A$ into the equation for area:
$A = l × w$
$12 = w(w + 4)$
Simplifying:
$12 = w^2 + 4w$
Subtracting $12$ from both sides:
$0 = w^2 + 4w − 12$, which can be factored as:
$(w + 6)(w − 2) = 0$
Since $w$ must be positive, we equate $w − 2$ to $0$ to get $w = 2$. Since $l = w + 4$, we find that $l = 6$.
$l = w + 4$
Substituting in $w + 4$ for $l$ and $12$ for $A$ into the equation for area:
$A = l × w$
$12 = w(w + 4)$
Simplifying:
$12 = w^2 + 4w$
Subtracting $12$ from both sides:
$0 = w^2 + 4w − 12$, which can be factored as:
$(w + 6)(w − 2) = 0$
Since $w$ must be positive, we equate $w − 2$ to $0$ to get $w = 2$. Since $l = w + 4$, we find that $l = 6$.
Question 11 |
$3^{−2}= \; ?$
$−9$ | |
$−6$ | |
$9$ | |
$\dfrac{1}{9}$ |
Question 11 Explanation:
The correct answer is (D). To evaluate a base raised to a negative exponent that is in the numerator, rewrite the expression with the base and exponent in the denominator, and rewrite the negative exponent as a positive exponent. In cases where the base raised to a negative exponent is in the denominator, rewrite the base and exponent in the numerator, and switch the sign of the exponent:
$a^{−n}=\dfrac{1}{a^n}$
$3^{−2}=\dfrac{1}{3^2}=\dfrac{1}{9}$
$a^{−n}=\dfrac{1}{a^n}$
$3^{−2}=\dfrac{1}{3^2}=\dfrac{1}{9}$
Question 12 |
$(3x + 4y)(2x + 5y) = \; ?$
$3x^2 + 8xy + 20y^2$ | |
$3x^2 + 15xy + 20y^2$ | |
$6x^2 + 15xy + 20y^2$ | |
$6x^2 + 23xy + 20y^2$ |
Question 12 Explanation:
The correct answer is (D). The “FOIL method” is the easiest way to remember how to multiply expressions of the form $(x + y)(a + b)$. Multiply the First two terms, then the Outer two terms, then the Inner two terms, and then the Last two terms, then sum all four to arrive at the answer:
$(3x + 4y)(2x + 5y)$
$6x^2 + 15xy + 8xy + 20y^2$
$6x^2 + 23xy + 20y^2$
$(3x + 4y)(2x + 5y)$
$6x^2 + 15xy + 8xy + 20y^2$
$6x^2 + 23xy + 20y^2$
Question 13 |
Which of the following is the equation of a line passing through the points $(0,8)$ and $(−4,0)$ on the $xy$-plane?
$y = 8x − 4$ | |
$y = 2x + 8$ | |
$y = − \dfrac{1}{2}x + 8$ | |
$y = −4x + 8$ |
Question 13 Explanation:
The correct answer is (B). All answers are expressed in slope-intercept form:
$y = mx + b$
$m = \dfrac{y_2 − y_1}{x_2 − x_1} = \dfrac{0 − 8}{−4 − 0}$ $ = \dfrac{−8}{−4} = 2$
The variable $b$ represents the $y$-intercept, which is actually given by the point $(0,8)$. When $x = 0, y = 8$. Thus, $b = 8$.
Substituting $m$ and $b$ into our equation yields:
$y = 2x + 8$
$y = mx + b$
$m = \dfrac{y_2 − y_1}{x_2 − x_1} = \dfrac{0 − 8}{−4 − 0}$ $ = \dfrac{−8}{−4} = 2$
The variable $b$ represents the $y$-intercept, which is actually given by the point $(0,8)$. When $x = 0, y = 8$. Thus, $b = 8$.
Substituting $m$ and $b$ into our equation yields:
$y = 2x + 8$
Question 14 |
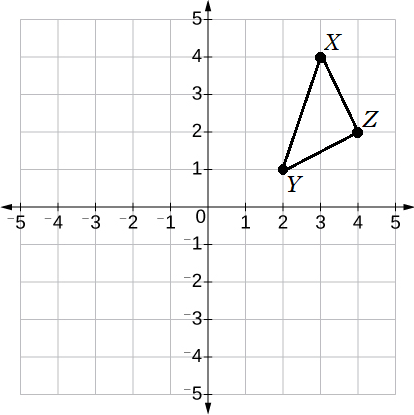
Triangle $XYZ$ lies in the $xy$-plane. The $(3,4)$, the coordinates of vertex $Y$ are $(2,1)$, and the coordinates of vertex $Z$ are $(4,2)$.
If the triangle is rotated 270° clockwise to produce triangle $X'Y'Z'$, what will be the coordinates of vertex $X'$ which corresponds to vertex $X$ of triangle $XYZ$?
$(−4,3)$ | |
$(3,−4)$ | |
$(−3,4)$ | |
$(4,−3)$ |
Question 14 Explanation:
The correct answer is (A). Rotating Triangle XYZ 270° clockwise is the same as rotating it 90° counter-clockwise (ccw). We are interested in determining where vertex $x$ lands after being rotated 90° ccw.
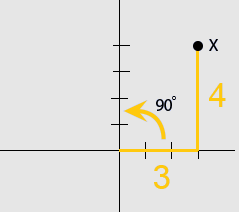
Position of $x'$ after $x$ has been rotated:
The coordinates of $x' = (−4, 3)$
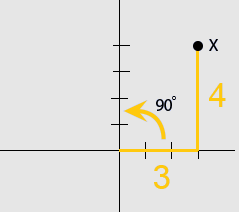
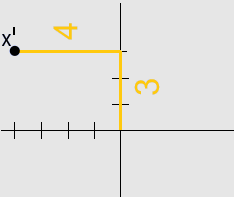
Position of $x'$ after $x$ has been rotated:

The coordinates of $x' = (−4, 3)$
Question 15 |
A rectangle is cut in half to create two squares that each have an area of 25. What is the perimeter of the original rectangle?
20 | |
25 | |
30 | |
35 |
Question 15 Explanation:
The correct answer is (C). The formula to find the area of a square is $\text{side} \times \text{side}$. If each square has an area of $25$, then the dimensions of the rectangle are $5 \times 10$.
The perimeter is the sum of all the sides, and would therefore be $5 + 10 + 5 + 10 = 30$.
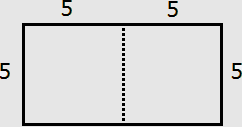
The perimeter is the sum of all the sides, and would therefore be $5 + 10 + 5 + 10 = 30$.

Question 16 |
If $f(x) = 4x^2$ and $g(x) = 5x$, what is $g(f(2x))$?
$100x^2$ | |
$80x^2$ | |
$20x^2$ | |
$10x^2$ |
Question 16 Explanation:
The correct answer is (B). First evaluate the inner function by substituting $2x$ into the expression for $f(x)$:
$f(2x) = 4(2x)^2$
$f(2x) = 4(4x^2)$
$f(2x) = 16x^2$
Next substitute the expression for $f(2x)$ into the expression for $g(x)$:
$g(f(2x)) = g(16x^2) \quad$ $\text{(Read as “g of } 16x^2”)$
$g(f(2x)) = 5(16x^2)$
$g(f(2x)) = 80x^2$
$f(2x) = 4(2x)^2$
$f(2x) = 4(4x^2)$
$f(2x) = 16x^2$
Next substitute the expression for $f(2x)$ into the expression for $g(x)$:
$g(f(2x)) = g(16x^2) \quad$ $\text{(Read as “g of } 16x^2”)$
$g(f(2x)) = 5(16x^2)$
$g(f(2x)) = 80x^2$
Question 17 |
In a coordinate plane, triangle ABC has the following coordinates:
$(−2,7),(−3,6),(4,5)$
If triangle ABC is reflected over the $y$-axis, what are the coordinates of the new image?
$(2,7), (3,6), (−4,5)$ | |
$(2,7), (3,6), (4,5)$ | |
$(7,−2), (6,−3), (5,4)$ | |
$(−2,−7), (−3,−6), (4,−5)$ |
Question 17 Explanation:
The correct answer is (A). One way to solve this problem is to draw the figure and then count how many units each point is from the $y$-axis, and to then count that many units in the opposite direction. A more efficient method is to recognize that reflecting over the $y$-axis causes the $x$-value to switch sign, but does not influence the $y$-value of the point.
According to the second method, reflecting $(−2,7)$, $(−3,6)$, $(4,5)$ across the $y$-axis produces the points $(2,7)$, $(3,6)$, $(−4,5)$.
According to the second method, reflecting $(−2,7)$, $(−3,6)$, $(4,5)$ across the $y$-axis produces the points $(2,7)$, $(3,6)$, $(−4,5)$.
Question 18 |
Which of these expressions is equivalent to $(x^7y^3)^5 \,$?
$x^{12}y^8$ | |
$x^{35}y^8$ | |
$x^8y^{12}$ | |
$x^{35}y^{15}$ |
Question 18 Explanation:
The correct answer is (D). The power is distributed to each term in the parenthesis:
$(x^7 × y^3 )^5$
$= x^{7 × 5}y^{3 × 5}$
$= x^{35} y^{15}$
$(x^7 × y^3 )^5$
$= x^{7 × 5}y^{3 × 5}$
$= x^{35} y^{15}$
Question 19 |
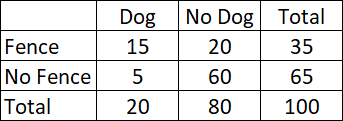
The table above shows the results of a 100-person survey. Each person was asked if they owned a dog and if their yard was fenced-in. Given that the person's yard is fenced, what is the probability that they own a dog?
$\dfrac{3}{7}$ | |
$\dfrac{1}{5}$ | |
$\dfrac{3}{4}$ | |
$\dfrac{3}{20}$ |
Question 19 Explanation:
The correct answer is (A). "Given that the person's yard is fenced" means we are only looking at the first row (highlighted).
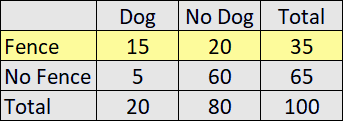
Looking only at this first row, the probability that the person owns a dog is:
$\dfrac{15}{35} = \dfrac{3}{7}$

Looking only at this first row, the probability that the person owns a dog is:
$\dfrac{15}{35} = \dfrac{3}{7}$
Question 20 |
Simplify:
$\dfrac{6x^5 − 2x − 4}{2x}$
$3x^4 − \dfrac{2}{x}$ | |
$\dfrac{3x^5 − x − 2}{x}$ | |
$3x^4 − 1 − \dfrac{2}{x}$ | |
$3x^4 + 1 − \dfrac{2}{x}$ |
Question 20 Explanation:
The correct answer is (C). Completely simplify the expression by dividing every term in the numerator by the term in the denominator:
$\dfrac{6x^5 − 2x − 4}{2x}$
$= \dfrac{6x^5}{2x} + \dfrac{−2x}{2x} + \dfrac{−4}{2x}$
$= 3x^4 − 1 − \dfrac{2}{x}$
$\dfrac{6x^5 − 2x − 4}{2x}$
$= \dfrac{6x^5}{2x} + \dfrac{−2x}{2x} + \dfrac{−4}{2x}$
$= 3x^4 − 1 − \dfrac{2}{x}$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 20 questions to complete.
|
List |
